Lecture 15: RNA-seq - Quantification and the EM algorithm

Lecture 15: RNA-seq - Quantification and the EM algorithm

Wednesday, May 18, 2016

Scribed by Paraskevas Deligiannis and revised by the course staff

Topics

In the previous lecture, we introduced RNA-seq and the quantification problem. In this lecture, we dive deeper into this problem – in the case when we know the RNA transcripts beforehand – and examine how we can solve it optimally under some simplicity assumptions.

1. The RNA quantification problem & our assumptions
2. Naive split reads
   • Shortcomings of naive splitting
3. Improved approach: Iterative estimation refinement
   • Basic Idea
   • General Algorithm
   • Questions
4. Maximum Likelihood estimation
   • Convexity
   • Special case: Uniquely-mapped reads
5. Expectation-Maximization (EM) algorithm
   • Key idea
   • Convergence & Optimality
   • Iterative steps
   • Application to our problem
   • “Hard” EM

The RNA quantification problem & our assumptions

As discussed in the last lecture, the RNA-seq data consist of multiple reads sampled from the various RNA transcripts in a given tissue (after the reverse transcription of RNA to cDNA). We assume that these reads are short in comparison to the RNA transcripts and have equal length \(L\).

We, also, assume that we know the list of all possible RNA transcripts \(t_1,t_2, \dots,t_K\) beforehand. Every read \(R_i,i=1,2,\dots,N \ \\) is mapped (using alignment) to (possibly multiple) transcripts. Our goal is to estimate the abundance of each transcript \(\rho_1, \rho_2,...,\rho_K, \\) where \(\rho_k \in [0,1], \ k \in \{1,2, \cdots, K \} \ \\) denotes the fraction of \(t_k\) among all transcripts.

Additionally, we make the following assumptions for the sake of simplicity:

• All transcripts have equal length \(\ell\). It is fairly straightforward to extend our analysis to transcripts of unequal length.
• The reads come from uniformly sampling all the transcripts. This is a relatively mild assumption we have made before to ease our analysis, even though it is not entirely accurate.
• Each read can come from at most one location on each transcript. This is a reasonable assumption, since different exons rarely contain common subsequences.

Naive split reads

As discussed in the previous lecture, the difficulty of the above counting problem lies in the existence of multiply-mapped reads. This occurs due to the fact that different transcripts can contain the same exons.

One approach to deal with these reads would be to split them, i.e. assign a fractional count to each transcript a read maps to. The simplest way to do this is by splitting the read equally among all transcripts it is mapped to. For instance, if a read maps to 5 transcripts, then each of them gets a count of \(\frac{1}{5}\).

Finally, our estimate of the abundance of \(t_k\) with total count \(N_k\) is

Shortcomings of naive splitting

While naive read splitting sounds reasonable, it can fail spectacularly as illustrated by the following example.

Transcripts sharing a common exon

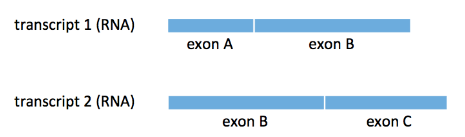
Here, we have two transcripts \(t_1, t_2\) sharing a common exon B and our ground truth is that \(\rho_1=1\) and \(\rho_2=0\). As a result, some of our \(N=20\) reads come from exon A and some come from exon B. Let’s assume that half of the reads come form each exon (even though the figure above does not depict the two exons as of equal length).

All the reads coming from exon A map uniquely to \(t_1\) and thus, they contribute a total of \(\frac{20}{2}=10\) to the count \(N_1\) of \(t_1\). All the \(\frac{20}{2}=10\) reads coming from exon B map to both transcripts and according to the naive algorithm above, each of them contributes \(\frac{1}{2}\) to each of the counts \(N_1, N_2.\) As a result, our estimate is that

which is clearly wrong.

Improved approach: Iterative estimation refinement

Since the naive algorithm fails, we need to come up with a better solution. We note that despite the failure, we came closer to the truth (in comparison to a random guess of equal abundances). Is there a way to leverage the information we gained?

Basic Idea

What if we were to use our newly obtained estimate of abundances to re-split the multiply-mapped reads with weights proportional to the relative abundances of the two transcripts? In our example, this would mean that

which is closer to the truth.

But now, we can simply repeat the process using the updated estimate of the abundances. It is easy to see that at each step, \(\hat{\rho}_2^{(m)}\) will be halved and hence, this process converges to the ground truth at an exponential rate.

This seems promising. So, let’s formulate this algorithm more generally.

General Algorithm

1. Since we know nothing about the abundances to begin with, our initial estimate is uniform. That is
   \[\hat{\rho}_k^{(0)}=\frac{1}{K},k=1,2,…,K\]

2. For step \(m=1,2,...\) repeat:

   • For \(i=1,2,..,N\) let read \(R_i\) map to to a set \(S_i\) of transcripts, denoted by \(R_i \to S_i\). Then, split \(R_i\) into fractional counts for each transcript \(k \in S_i\), equal to the relative abundances of the transcripts in \(S_i\), as follows:
     \(f_{ik}^{(m)}=\begin{cases} \frac{\rho_k^{(m)}}{\sum_{j \in S_i}{\rho_j^{(m)}}} &\text{if }k \in S_i \\ 0 & \text{otherwise} \end{cases}\)
   • The updated estimate is, obviously,
     \(\hat{\rho}_k^{(m+1)}=\frac{1}{N}\sum_{i=1}^{N}{f_{ik}^{(m)}}\)

Questions

The natural questions that arise now are

1. whether this algorithm converges in general and
2. even if it does, does it converge to the Maximum Likelihood (ML) estimate \(\mathbf{\hat{\rho}^{ML}}\)?

The former is crucial, since a non-converging process is, basically, useless. The latter examines the performance of the algorithm in terms of estimation accuracy. Given that we have a finite amount of data, we cannot guarantee that the ground truth is recovered. Our best hope is to find \(\mathbf{\hat{\rho}^{ML}}\).

This leads us to our next few topics. What is \(\mathbf{\hat{\rho}^{ML}}\) and how can we compute it efficiently?

Maximum Likelihood estimation

Let \(\mathbf{\rho}=[\rho_1\ \rho_2\ ...\ \rho_K]^T \\) be the vector of transcript abundances. The distribution of the reads depends on \(\mathbf{\rho}\). Since the reads are sampled independently, we have that

We note that \(R_i=r_i\) if and only if the read \(R_i\) maps to a transcript \(t_k\) that contains the sequence \(r_i\) and \(R_i\) starts from the same position as \(r_i\). (Recall our assumption that each read can come from at most one location on each transcript.) Therefore, the probability

The reads are sampled uniformly, so \(Pr(R_i\ maps\ to\ t_k;\mathbf{\rho})=\rho_k\). Also, each transcript \(t_k\) has length \(l\) and each read of length L coming from \(t_k\) has an equal chance of starting at each of the possible \(l-L+1\) positions, hence

Finally, let

As a result,

which means that

Maximizing the likelihood function is equivalent to maximizing the log-likelihood, and since \(-N\log{(l-L+1)}\) is a constant, the ML estimation for \(k=1,...,K\) is

If we define the matrix \(Y \in \{0,1\}^{N \times K}\) with elements \(y_{ik}\), then

Along each row \(i\) of matrix \(Y\) the positions with value 1 represent the transcripts to which \(R_i\) maps. Along each column \(k\) of \(Y\), the positions with value 1 represent the reads that map to \(t_k\).

As we can see, the effect of the data (reads) on the ML estimate can be summarized by matrix \(Y\), or equivalently, its entries \(y_{ik}\). Therefore, \(Y\) is a sufficient statistic for this ML inference problem.

Convexity

The above maximization problem is a convex optimization problem, which is desired, since convex problems are well studied and there exist tools to solve them efficiently.

The convexity arises from the combination of the following factors:

• it involves the maximization of a concave objective function, as

  • \(\sum_{k=1}^K{y_{ik}\rho_k}\) is an affine function of \(\mathbf{\rho}\)

  • \(\log(\cdot)\) is concave

  • the composition of a concave with an affine function is concave

  • the sum of concave functions is concave

• both \(\rho_k \ge 0\) and \(\sum_{k=1}^K{\rho_k}=1\) are linear constraints

Special case: Uniquely-mapped reads

Let’s consider the special case when there are no multiply-mapped reads, i.e. every read maps to at most one transcript, or equivalently, each row of matrix \(Y\) has at most one element with value 1. If we denote by \(N_k\) the number of reads that map to transcript \(t_k\), then the above maximization problem becomes

This problem is easy to solve by equating to 0 the gradient of the objective function w.r.t \(\mathbf{\rho}\) and using Lagrange multipliers. The result is obvious and reassuring:

After all, we knew that the naive approach with split reads works when all reads are uniquely mapped. Note that when all reads map to exactly one transcript, \(\sum_{k=1}^K{N_k}=N\).

Expectation-Maximization (EM) algorithm

The EM algorithm was thoroughly described in a 1977 article written by Arthur Dempster, Nan Laird, and Donald Rubin. It provides an iterative method to compute – locally optimal – ML parameters of a statistical model. If \(\mathbf{\theta}\) denotes the unknown parameters to be estimated (in our case, \(\mathbf{\rho}\)) and \(\mathbf{x}\) are the observed variables (data, in our case, the reads), then the EM algorithm computes

Key idea

The basic observation is that in many cases of statistical inference, the problem would become significantly easier, or even trivial, if we knew some unobserved hidden variable(s) \(Z\). For instance, in our case, if we somehow knew for every read which transcript it came from, then our problem would reduce to the simple problem with uniquely mapped reads. This information can be represented by a matrix \(Z\) such that

The idea behind EM is to iteratively try to use \(\mathbf{x}\) and the current estimate \(\mathbf{\hat{\theta}}\) to compute the posterior distribution: \(p(Z \mid \mathbf{x} ,\mathbf{\hat{\theta}})\). Then we update our estimate \(\mathbf{\hat{\theta}}\) to maximize the expected value of the likelihood \(p(\mathbf{x},Z \mid \mathbf{\theta})\) w.r.t. \(p(Z\mid\mathbf{x};\mathbf{\hat{\theta}})\) and so on:

Convergence & Optimality

It is proven that the EM algorithm always improves the likelihood \(Pr(\mathbf{x};\mathbf{\hat{\theta}})\) at every iteration. Since \(Pr(\mathbf{x};\mathbf{\theta})\) is bounded above by 1, this means that the EM algorithm converges to a local maximum.

However, we saw from our ML analysis in a previous section that the ML optimization problem is concave. This means that there is only one local maximum, the global one. Thus, the EM algorithm is guaranteed to find the optimal ML estimate.

Iterative steps

Let’s formally describe the EM algorithm. The algorithm consists of two successive steps, the expectation step (E step) and the maximization step (M step), after which it is named. These steps are repeated until the algorithm converges.

For iteration \(m = 0,1,2,...\)

1. E step: Compute the expected value of the log-likelihood function w.r.t the conditional distribution of \(Z|\mathbf{x}\) using the current estimate of the unknown parameters \(\mathbf{\hat{\theta}^{(m)}}\):
   \(J(\mathbf{\theta};\mathbf{\hat{\theta}^{(m)}}) = \mathbb{E}_{Z|\mathbf{x};\mathbf{\hat{\theta}^{(m)}}}[\log{p(\mathbf{x},Z|\mathbf{\theta})}]\)

2. M step: Find the updated estimate \(\mathbf{\hat{\theta}}\) that maximizes \(J\):
   \(\mathbf{\hat{\theta}^{(m+1)}} = \argmax_{\mathbf{\theta}}{J(\mathbf{\theta};\mathbf{\hat{\theta}^{(m)}})}\)

Application to our problem

In our case, it is easy to see that the probability that a read \(R_i \to S_i\) comes from the transcript \(t_k\) is proportional to the relative abundance of \(t_k\) in \(S_i\). Namely, given our reads \(\mathbf{R}\) and our current estimate \(\mathbf{\rho}^{(m)}\),

We have that

where in the first step, we note that since \(Z\) represents the ground truth, there is at most one non-zero term in the sum \(\sum_{k=1}^K{Z_{ik}}\) (similar to the case with uniquely mapped reads). We drop the indicator function in the second step assuming that \(\mathbf{R}\) and Z are consistant.

Consequently,

where we have omitted the linear constraints on \(\mathbf{\rho}\) for simplicity. One can verify that if we define \(\hat{N}_k = \sum_{i=1}^N{f_{ik}^{(m)}}\), the above results follow readily from our analysis for the case of uniquely mapped reads. This is, after all, the reason why we use the hidden variable \(Z\).

“Hard” EM

The EM algorithm described above is a type of soft EM in the sense that at each iteration, it calculates and uses only an estimate of the distribution of \(Z\) given \(\mathbf{x};\mathbf{\theta}\).

In contrast, a hard EM algorithm would compute an estimate \(\hat{Z}\) of the values of \(Z\) and then use it to assign each read \(R_i \to S_i\) to the transcript \(t_k \in S_i\) that is most abundant according to the current estimate \(\mathbf{\hat{\rho}_k}\). The hard algorithm commits a lot more to its estimates than the “soft” alternative but seems simpler to implement.

Given its possible benefits over the soft version, the questions that arise are:

1. Will it work for the example of section shortcomings of naive splitting where there is a common exon in two different transcripts?
2. Will it work in general?